1️⃣ AVL 트리와 Red-Black 트리등이 등장하게 된 배경
BST 즉 이진 탐색 트리(Binary Search Tree)는 삽입 삭제를 계속 하다보면 균형이 안맞는 경우가 생깁니다.
그래서 이를 해결하기 위해 트리의 균형을 맞춰주는 AVL트리, Red-Black트리 B+트리 등이 등장하게 되었습니다.
그럼 오늘은 먼저 그 중 하나인 AVL 트리에 대해 알아보는 시간을 갖도록 하겠습니다.
2️⃣ AVL 트리란?
AVL 트리는 이진 탐색 트리의 최악 시간 복잡도 O(N)을 개선하고자 만들어진 트리입니다.
AVL 트리를 사용하면 삽입, 삭제, 탐색 모두 O(log N)의 시간 복잡도로 수행이 가능합니다.
AVL 트리의 정의는 다음과 같습니다.
모든 노드에 대해서 노드의 왼쪽 부트리와 오른쪽 부트리의 높이차가 1이하인 이진 탐색 트리
좀 더 알기 쉽게 아래 그림을 한번 살펴보겠습니다.
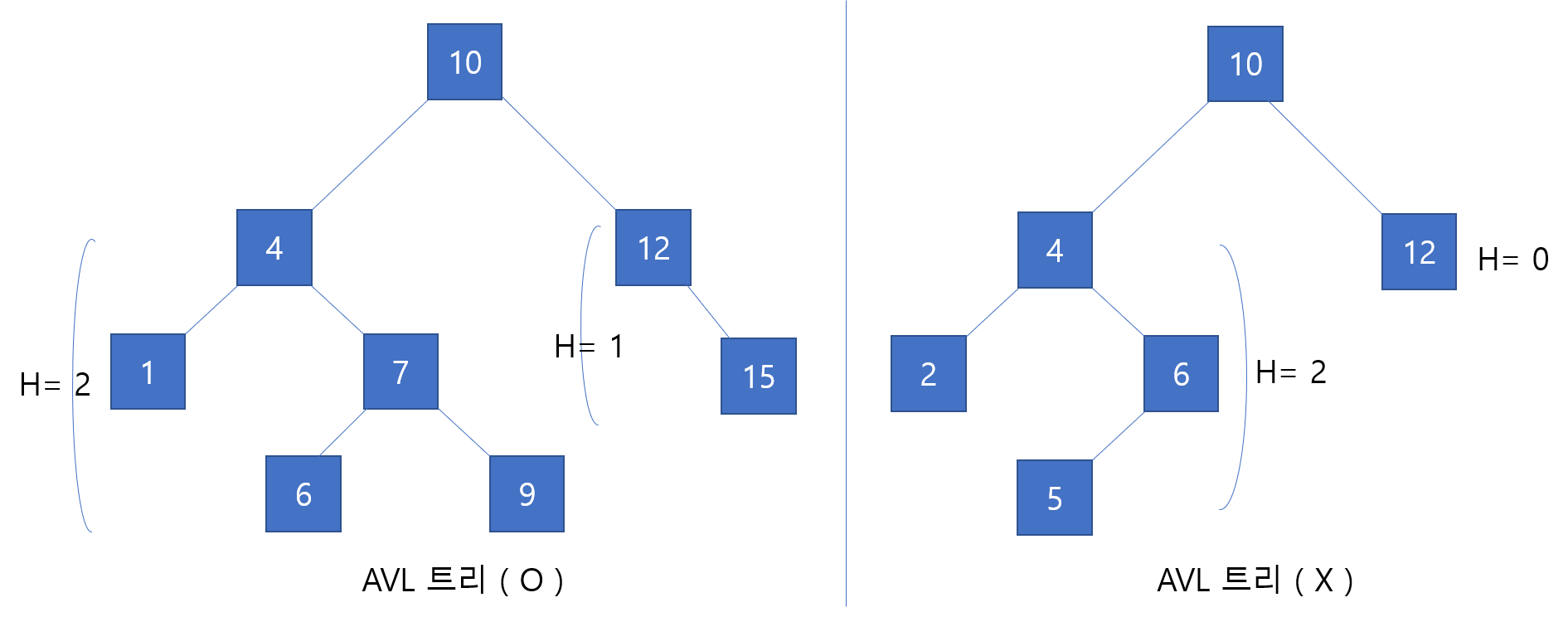
먼저 왼쪽 트리는 그 어떤 노드를 기준으로 해도 왼쪽 부트리와 오른쪽 부트리의 높이차가 1이하를 넘지 않습니다.
따라서 이 트리는 AVL 트리라고 불릴 수 있습니다.
하지만, 오른쪽 트리는 루트노드 10을 기준으로 보았을 때, 왼쪽 부트리는 높이가 2이고 오른쪽 부트리는 높이가 0이어서 AVL 트리라고 할 수 없습니다.
이러한 AVL 트리의 불균형의 종류는 무엇이 있을까요?
3️⃣ AVL 트리 불균형 종류와 해결방식
AVL 트리는 불균형을 회전(Rotation)이라는 작업을 통해 해결합니다.
이 회전의 종류는 left rotation, right rotation 이렇게 두가지 종류가 있습니다.
그림으로 두가지 회전에 대해 익혀보도록 합시다.
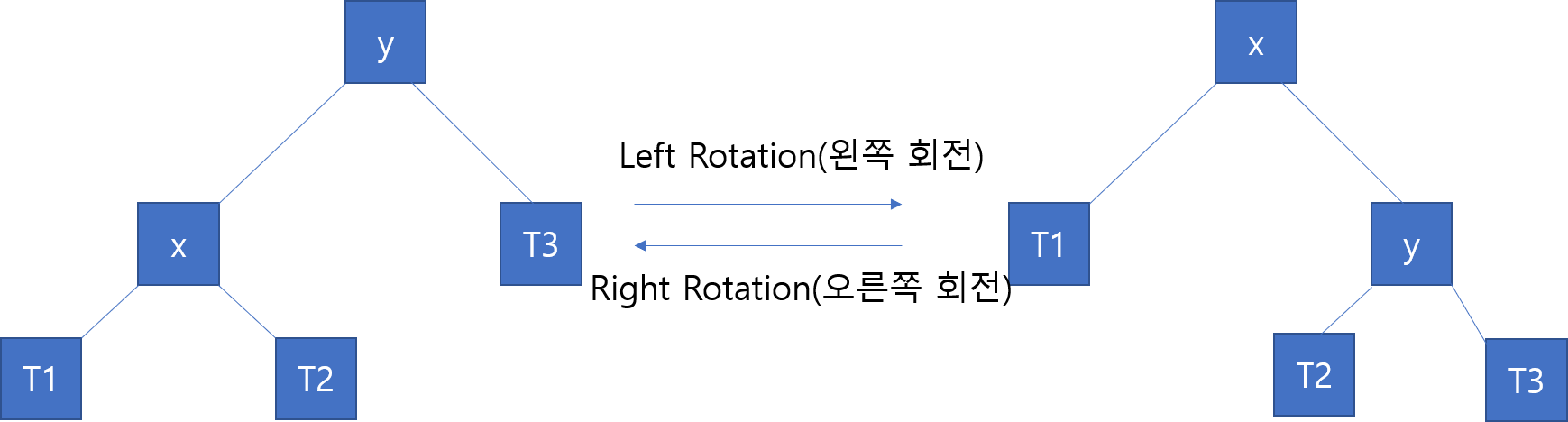
위의 트리는 다음과 같은 조건을 갖습니다. keys(T1) < key(x) < keys(T2) < key(y) < keys(T3)
AVL 트리 불균형의 종류는 총 4가지로 다음과 같습니다.
원소 x,y,z를 위주로 봐주시면 좋을 것 같습니다.
-
Left Left Case :
z 에서부터 y x로 가려면 왼쪽으로 두번가야된다고 해서 left left입니다. 이 방식은오른쪽 회전을 한번 해주면 해결됩니다. 아래 그림과 같습니다.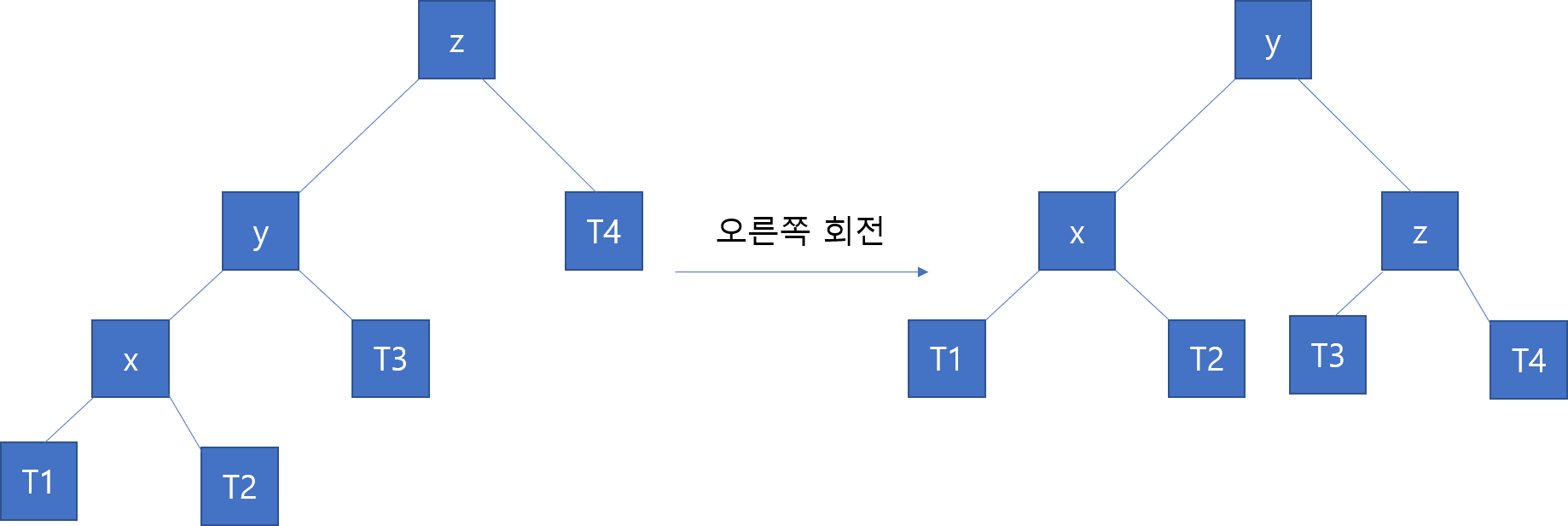
-
Left Right Case :
z 에서 x로갈때 left right로 가야해서 left right입니다. 이 방식은왼쪽으로 회전 후 오른쪽으로 한번 더 회전을 하면 균형이 잡히게 됩니다. 아래 그림과 같습니다.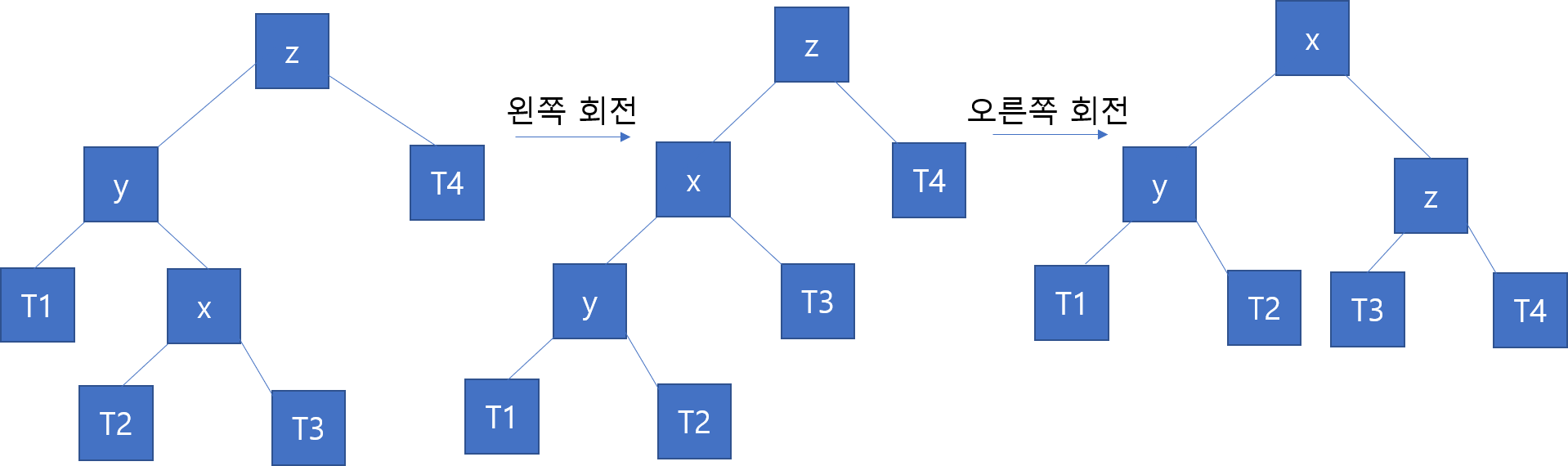
-
Right Right Case :
z 에서 x로갈때 오른쪽으로 두번 가야 해서 right right입니다. 이 방식은왼쪽 회전을 한번 해주면 불균형이 해결됩니다. 아래 그림과 같습니다.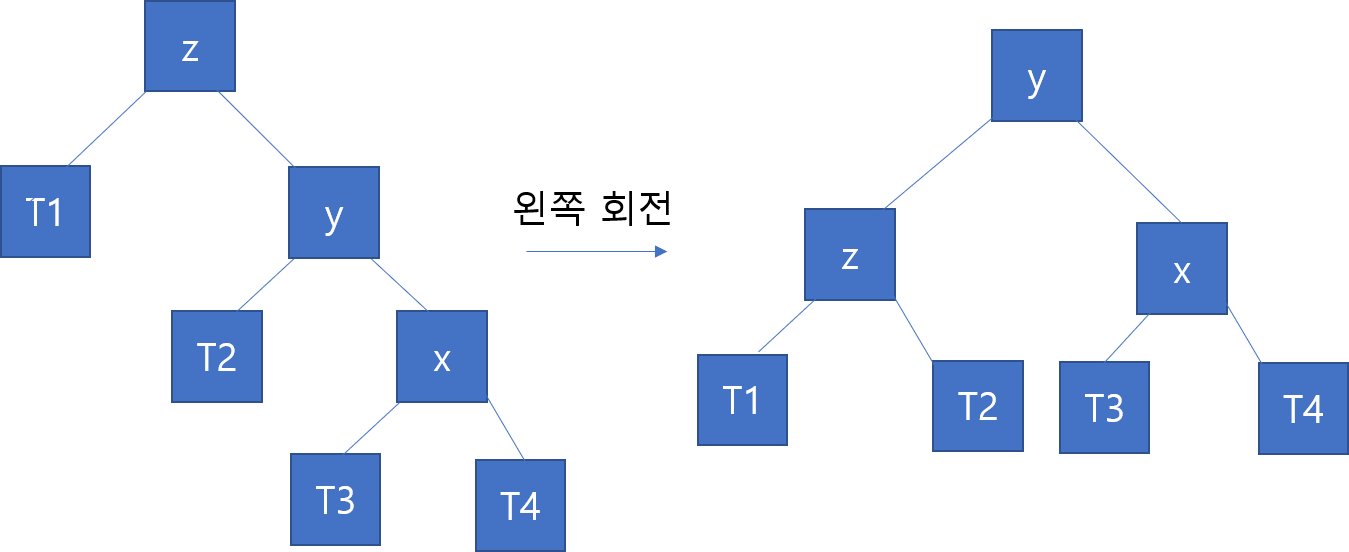
-
Right Left Case :
z에서 x로 갈때 오른쪽으로 한번 왼쪽으로 한번 가야해서 right left입니다. 이 방식은오른쪽 회전 후 왼쪽으로 회전을 하면 불균형이 해결됩니다. 아래 그림과 같습니다.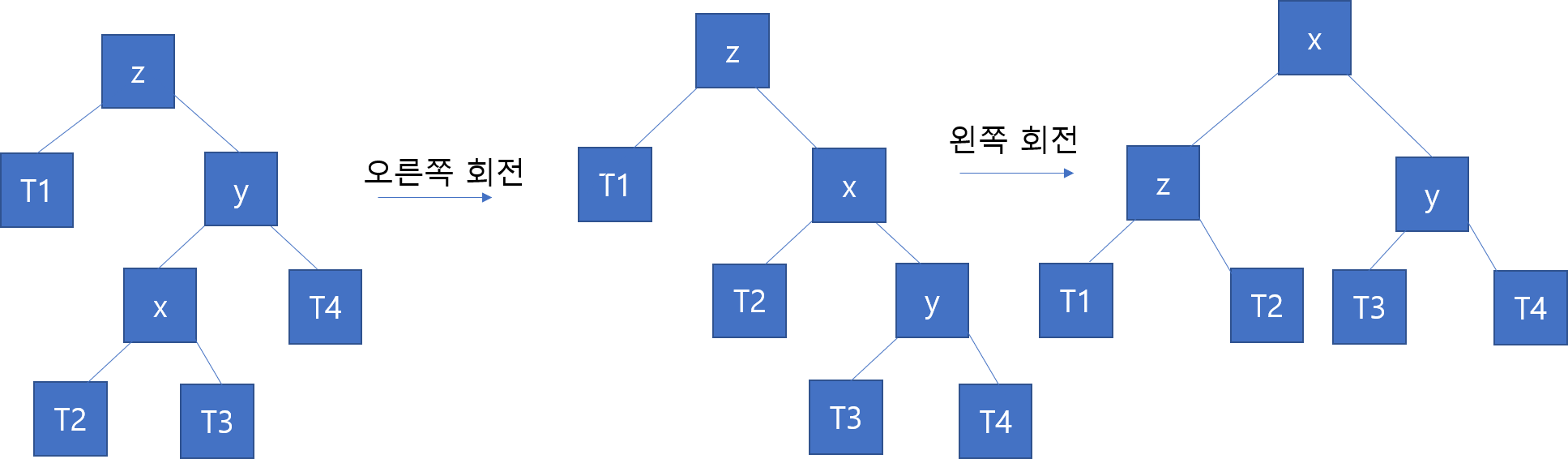
이 과정을 정리하자면 다음과 같습니다.
4️⃣ AVL 트리의 구현
AVL 트리의 구현은 Geeks for Geeks의 코드를 가져와서 한번 뜯어보는 시간을 가져보겠습니다.
아래 예제에서는 노드의 삽입 예제만 다루도록 하겠습니다.
삭제 예제는 Geeks for Geeks 이 링크를 참조해주세요.
아래는 삽입 코드와 주석입니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
# AVL트리 안에 노드를 삽입하는 코드
# 일반적인 트리 노드 클래스
class TreeNode(object):
def __init__(self, val):
self.val = val
self.left = None
self.right = None
self.height = 1
# 삽입 연산을 지원하는 AVL 트리 클래스
class AVL_Tree(object):
# 서브트리에 키를 삽입하고
# 서브트리의 새로운 루트를 리턴하는 재귀함수 입니다.
# 과정은 다음과 같습니다.
# 1. 노드를 삽입하고, 루트로 올라가면서 높이를 업데이트 합니다.
# 2. 업데이트하려는 노드의 양쪽 자식의 높이 차이가 2가 된다면,
# 이 노드를 X라 하고 X의 두 자식 중 높이가 큰 쪽을 y, y의 두 자식 중 높이가 큰 쪽을 z라고 합니다.
# 3. x, y, z를 대소관계에 따라 잘 재배치합니다.
def insert(self, root, key):
# Step 1 - 일반적인 이진탐색트리 만들기
if not root:
return TreeNode(key)
elif key < root.val:
root.left = self.insert(root.left, key)
else:
root.right = self.insert(root.right, key)
# Step 2 - 조상노드의 높이 업데이트
root.height = 1 + max(self.getHeight(root.left),
self.getHeight(root.right))
# Step 3 - 밸런스 요소 찾기
balance = self.getBalance(root)
# Step 4 - 노드가 불균형이면 4가지 케이스중 하나를 실행
# Case 1 - Left Left
if balance > 1 and key < root.left.val:
return self.rightRotate(root)
# Case 2 - Right Right
if balance < -1 and key > root.right.val:
return self.leftRotate(root)
# Case 3 - Left Right
if balance > 1 and key > root.left.val:
root.left = self.leftRotate(root.left)
return self.rightRotate(root)
# Case 4 - Right Left
if balance < -1 and key < root.right.val:
root.right = self.rightRotate(root.right)
return self.leftRotate(root)
return root
def leftRotate(self, z):
y = z.right
T2 = y.left
# 회전 수행
y.left = z
z.right = T2
# 높이 업데이트
z.height = 1 + max(self.getHeight(z.left),
self.getHeight(z.right))
y.height = 1 + max(self.getHeight(y.left),
self.getHeight(y.right))
# 새로운 루트 리턴
return y
def rightRotate(self, z):
y = z.left
T3 = y.right
# 회전 수행
y.right = z
z.left = T3
# 높이 업데이트
z.height = 1 + max(self.getHeight(z.left),
self.getHeight(z.right))
y.height = 1 + max(self.getHeight(y.left),
self.getHeight(y.right))
# 새로운 루트 리턴
return y
def getHeight(self, root):
if not root:
return 0
return root.height
def getBalance(self, root):
if not root:
return 0
return self.getHeight(root.left) - self.getHeight(root.right)
def preOrder(self, root):
if not root:
return
print("{0} ".format(root.val), end="")
self.preOrder(root.left)
self.preOrder(root.right)
myTree = AVL_Tree()
root = None
root = myTree.insert(root, 10)
root = myTree.insert(root, 20)
root = myTree.insert(root, 30)
root = myTree.insert(root, 40)
root = myTree.insert(root, 50)
root = myTree.insert(root, 25)
"""AVL 트리는 최종적으로 다음과 같이 보일것입니다.
30
/ \
20 40
/ \ \
10 25 50"""
# 전위 순회 출력
myTree.preOrder(root)
# This code is contributed by Ajitesh Pathak
5️⃣ AVL 트리 시간복잡도
AVL 트리의 시간복잡도는 귀납법으로 증명이 가능합니다.
전체 높이가 h인 AVL 트리(이진균형트리)를 만족하기 위한 높이 레벨에서의 최소한의 노드 수를 T(h)라고 해봅시다.
T(1) = 1 입니다. T(2) = 2 입니다. 트리를 그려보시면 쉽게 알 수 있습니다. T(3) = 4 입니다. T(4) = 7 입니다.
이렇게 쭉 가다보면 T(h) = T(h-1) + T(h-2) + 1 (h>=3) 을 도출해내실 수 있습니다.
여기서 $T(h) \geq 2^{h/2-1}$을 귀납법으로 증명해봅시다.
- h = 1,2 일 때 성립합니다.
- h = k,k+1일 때 성립한다고 하면 (k≥1)
$T(k+2)=T(k+1)+T(k)+1 \geq 2^{(k+1)/2-1}+2^{k/2-1}+1 \geq 2⋅2^{k/2−1}=2^{(k+2)/2-1}$
또한 성립합니다.
따라서, $n \geq T(h) \geq 2^{h/2-1}$ 이므로, $2 \leq 2logn+2$입니다.
따라서 시간복잡도는 O(h) = O(logn)임을 알 수 있습니다.
6️⃣ 마치며
오늘은 이진탐색트리의 불균형을 해결한 트리인 AVL 트리를 알아보았습니다.
다음에는 또 다른 불균형 해결 트리인 Red-Black 트리에 대해 알아보도록 하겠습니다.
틀린 부분이나 궁금한 점이 있다면 아래 댓글 남겨주세요.
읽어주셔서 감사합니다.